Dicision Tree

Information Theory

• 정보량을 수치화하고 그것의 연산을 가능하게 하는 것

Quantity of Information 정보량

• 불확실성
• 확률이 낮은 사건일수록 정보량 (불확실성)은 높다
• 확률과 정보량은 반비례관계
• “오늘 하루 종일 맑다”
  • ‘내일은 맑다’ 의 불확실성
  • ‘내일은 큰 비가 온다’ 의 불확실성

Information Entropy

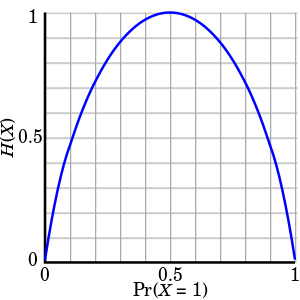
H(X)가 정보 엔트로피 값이고, 아래 축은 시행에서 어떤 사건이 일어날 확률입니다. 확률이 0.5일 때 엔트로피가 가장 높은 1임을 볼 수 있고, 확률이 한 쪽으로 편향될수록 엔트로피가 낮아지는 것을 볼 수 있습니다.

• 확률 변수의 정보량
• 얻은 정보가 의미있는 정보인지 (정보량)를 판단
• 가장 랜덤일 경우 엔트로피는 1 (최대)
• 아닐 경우 1 이하. 고정일 경우 0

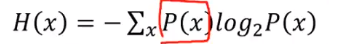
상호정보량 Mutual Information

• 하나의 확률변수가 다른 확률변수에 대해 제공하는 정보의 양

Decision Tree

• 분류, 회귀에서 사용
• 트리 형태로 의사결정 지식을 표현한 것

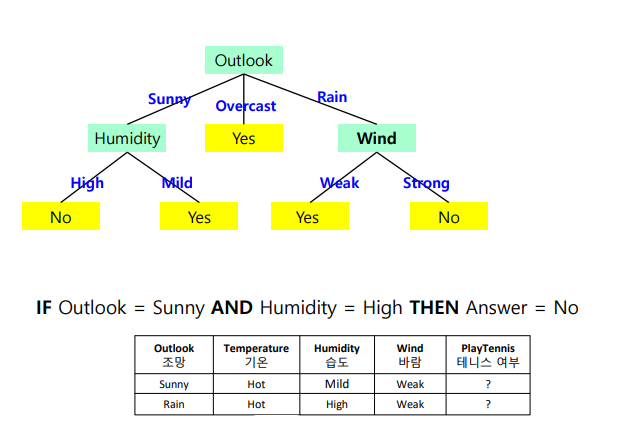
• 내부 노드 : 비교 속성
• 단말 노드 (ternimal node) : 기대값
• 간선 (edge) : 속성 값

Decision Tree알고리즘

• 반복적인 노드 분할 과정
  • 분할 속성 (spliting attribute) 을 선택
  • 속성값에 따라 서브트리를 생성
  • 데이터를 속성값에 따라 분배

분할속성 결정 방법

Information Gain (정보 이득)

• 어떤 분류를 통해 얼마나 information에 대한 이득이 생겼는지를 나타냄
• Entropy를 통해 계산
• 어떤 Feature를 선택함으로써 더 데이터를 잘 구분하는지

엔트로피 계산

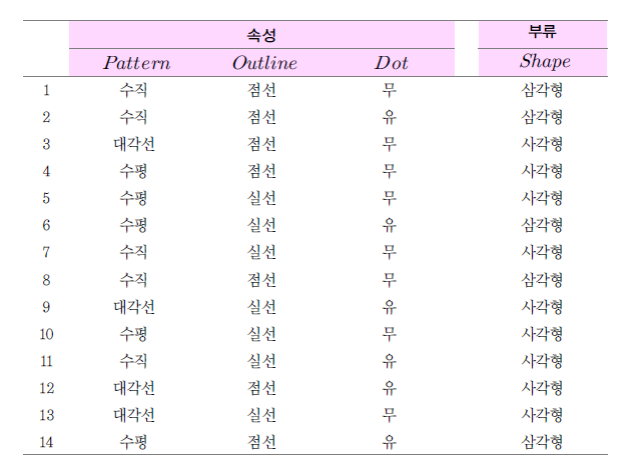
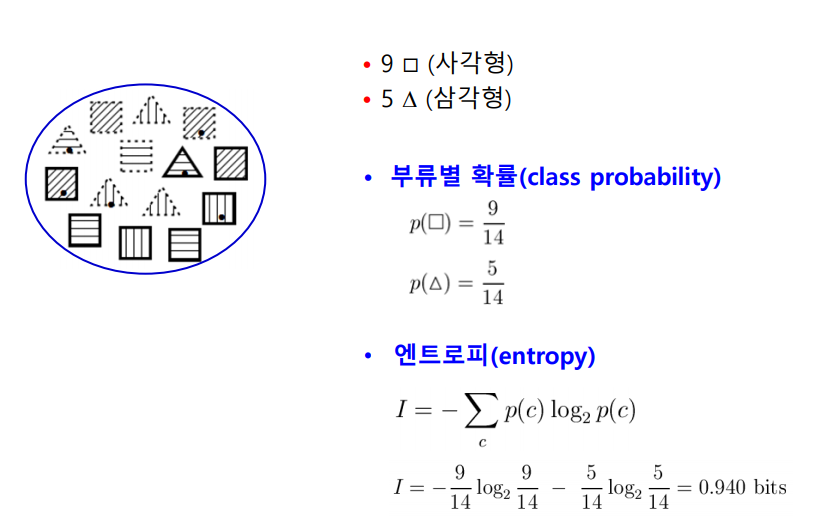
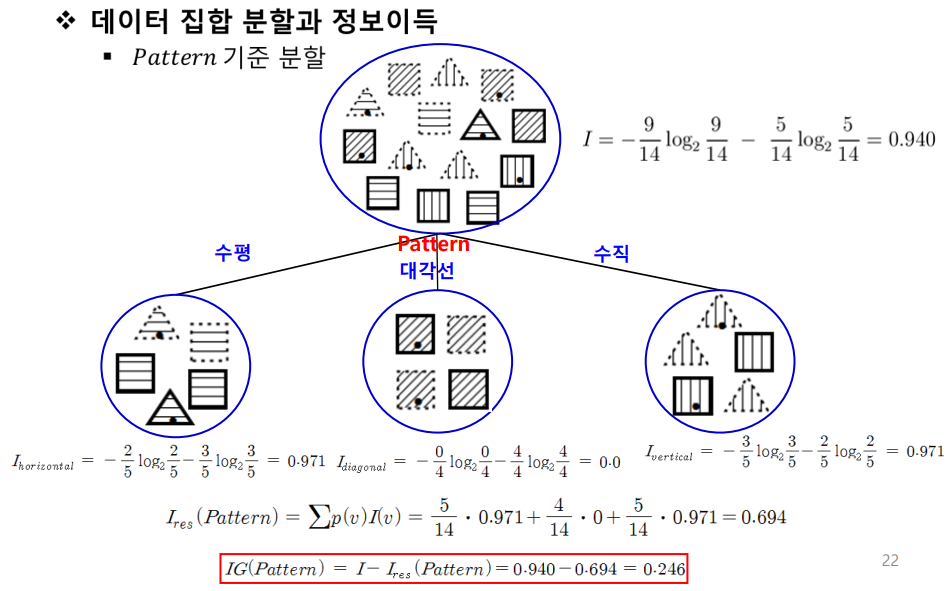
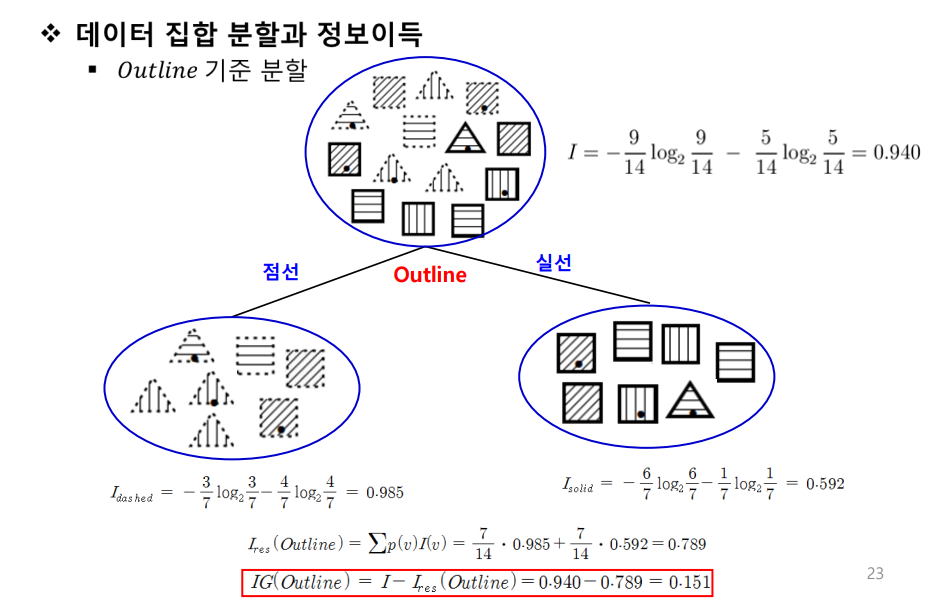
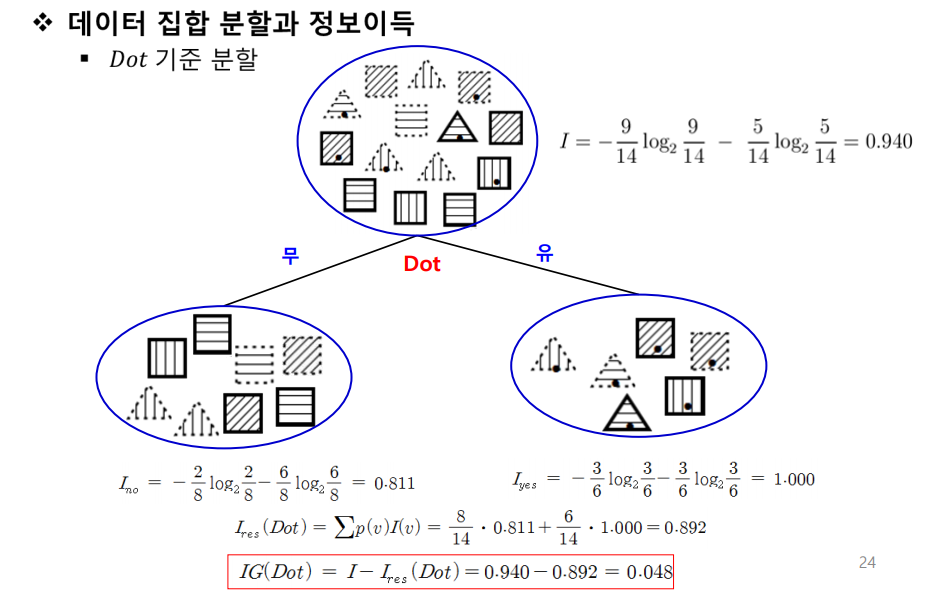
속성별 정보이득

• IG(Pattern) = 0.246
• IG(Outline) = 0.151
• IG(Dot) = 0.048

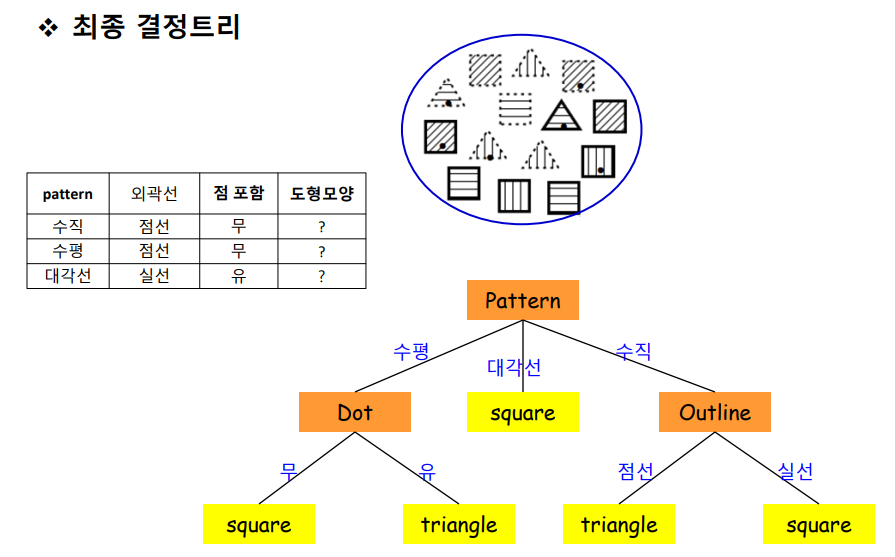
분할속성 선택

• 정보이득이 큰것 선택
  • Pattern 선택

Decision Tree 개선 척도

• 정보이득비 (빠르게 건너뜀)
• 지니지수 (빠르게 건너뜀)

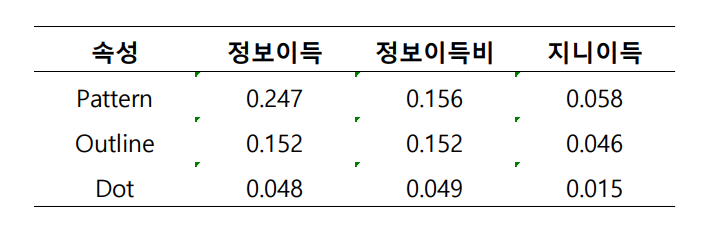
분할속성 평가 척도 비교

결정트리 알고리즘

• ID3
  • 범주형 속성값을 갖는 데이터
• C4.5
  • 범주형 + 수치형 속성값
  • ID3을 개선
• CART
  • 수치형 속성값

앙상블 Ensemble Classifier

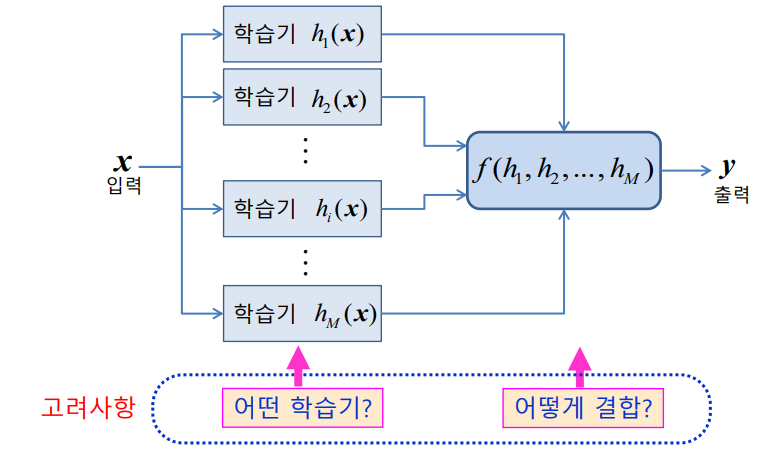
학습기 결합

• 선형 분류기와 같은 간단한 인식기로 학습을 수행
• 복수 개의 선형 분류기의 학습 결과를 결합해 좋은 성능의 인식기를 만듬

장점

• 나쁜 운을 피할 수 있다
• 성능향상
• 데이터 양, 질에 따른 어려움 극복
• 결정 경계가 너무 복잡한 경우 사용

결합

• 병렬적 결합
  • 한번에 일괄로 분류하여 최종 결과 생성
• 순차절 결합
  • 각 분류기의 결과를 순차적으로 조합

결합 방법의 분류

• Filter에 의한 방법 (순차)
  • 각 분류기 학습때마다 새로운 데이터를 생성
  • Boosting, Cascading
• Resampling에 의한 방법 (병렬)
  • 주어진 전체 데이터로부터 일부 집합을 추출하여 각 분류기를 학습
  • Bagging, MadaBoost
• Rewrighting에 의한 방법
  • 모든 분류기에 대해 동일한 학습 데이터 사용 → 각 데이터에 가중치를 부여해 학습에 대한 영향도 조절
  • AdaBoost

배깅 (Bagging, bootstrap aggregating)

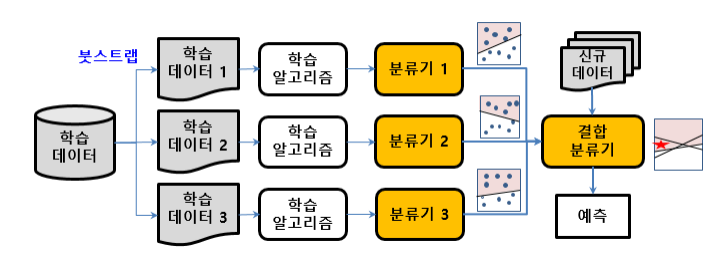
• 부트스트랩을 통해 여러개의 학습데이터 집합을 만들고, 각 학습 데이터 집합별로 분류기를 만들어 이들이 투표나 가중치 투표를 하여 최종 판정

랜덤 포레스트 (Random Forest)

• 분류기로 결정트리를 사용하는 배깅 기법

부스팅 (Boosting)

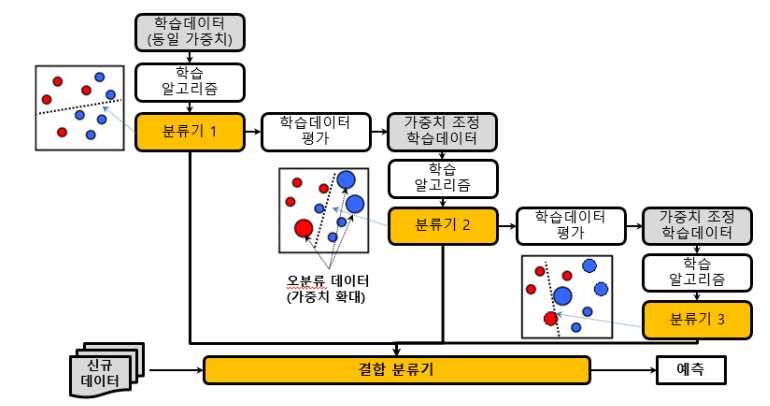
• K개의 분류기를 순차적으로 만들어가는 앙상블 기법
• 분류 정확도에 따라 학습데이터에 가중치를 변경해가면서 분류

AdaBoost

• 검색필요